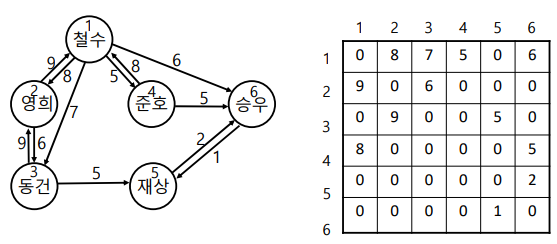
알고리즘 = 9세기경 페르시아 수학자 알콰이즈미의 이름에서 유래된 최초의 알고리즘 = 유클리드의 최대 공약수 알고리즘입니다. 그럼 알고리즘이란 무엇인가?어떤 문제를 해결하기 위한 단기적인 절차, 어떤 문제를 해결하기 위해 순서적으로 작성해놨다고도 이야기하고, 어떤 문제를 해결하기 위한 다양한 동작의 모형을 동작한 것, (간단하게) 단계적인 절차에 따라서… 하지만 단계적으로 순서대로 하는 것이 비효율적이기도 한 용어, 정당성과 정지성 = 정당성 같은 경우 올바른 결과를 반환해야 합니다. 이것이 정당성입니다, 정지성은 반드시 언젠가는 정지해야 합니다. 유한성…=반드시 정지한 후 알고리즘은 정해진 시간 내에 정확한 결과를 얻어야 한다.알고리즘의 기초-순서 구조-선택 구조-반복 구조 프로그래밍 언어를 배울 때 세 가지 구조에 대해 배웁니다.순서 구조의 경우는 순서대로 진행됩니다.선택구조 =어떤 조건에 따라 선택을 하고 옳을 때 또는 그렇지 않을 때 선택하는 선택구조 조건에 따라 처리의 흐름이 달라지는 것이 선택구조 반복구조 = for whilereturn 어떤 처리를 함에 있어 반복 반복적으로 수행하는데 조건이 성립하는 동안 반복되는 구조를 말합니다.그래서 알고리즘의 기초가 되지 않을까… 그러면 알고리즘의 다양한 종류 = 다양한 종류 기술 계산 정렬 검색 문자열 패턴 매칭 = 기술 계산부터 살펴보겠습니다. 유클리드 호제법 (최대 공약스) 가우스 소거법 (방정식) 사다리꼴의 법칙 (정적분) 다엑스트라 알고리즘 (최적경로) *이것을 곱한다 = 다엑스트라 이것은 다른 교재에서는 데이크스타라고도 불리는데요 ㅎㅎ 일단 유클리드 호제법 최적의 교재를 찾는 다엑스트라 알고리즘 에라토스테네스의 체 (소수) 소수를 구하는 기술계산 –>정렬같은 경우 단순 교환정렬 = 버블정렬 단순삽입정렬 = 쉘정렬-퀵정렬, 검색부분 내 데이터가 많은데? 원하는 것을 찾기 위한 알고리즘 선형검색그럼 오늘 수업에 들어갈 내용 오늘은 어떤 것인가? 알고리즘은어떤것이고대략적으로설명한것처럼이름을붙여서배우기전에이렇게풀고아이는보통이렇게이야기를해요.라는예정알고리즘1.최대숫자찾기(순차탐색):최대숫자찾기순서탐색1.2임의숫자찾기:임의숫자이지만바이너리탐색법이라고생각하시면됩니다.세 번째 동전의 거스름돈, 1.3 동전의 거스름돈: 그리드 알고리즘 1.4 붓글씨: 연필을 두드리지 않고 그림을 그림의 아이를 첫 시작점으로 마지막으로 돌아가야 한다(수학 문제로 대충 한 번만 건너가는 방법 등) 1.5 미로 찾기: 1.6 가짜 동전 찾기: 가짜 동전 찾기는 분할해서 무언가를 처리하는 정보, 그래서 분할 정보 알고리즘이라고 합니다.1.7 독이 든 술독: == 1.1 최대 숫자 찾기 10장의 카드 중 가장 큰 숫자를 찾아라… 카드의 모든 숫자가 표시되는 숫자가 반전, 45206055903575107525 카드의 숫자를 하나씩 비교하면서 생각한다, 그러니까 마지막 숫자를 보고 마지막에 결과의 이야기 가능 순서 탐색= 순서대로 읽으면서 찾는 방법, 그러면 굉장히 시간도 많이 걸리는 순차 탐색=SequentialSearch 임의의 숫자를 찾는다?이렇게 하면 순차탐색이긴 하지만 이진탐색을 2개씩 비교해서 찾는 임의의 숫자:85를 찾으라고 하면 어떻게 하겠습니까?45206035105908575252개를비교하고4520또비교2개씩비교를해보는거죠.그러면 비슷하죠?아이도 마찬가지입니다, 하나씩 읽으면서 책순으로 펼치면 좋겠는데, 카드가 10장 쌓이면 어떻게 할까…?그 다음 최대 숫자가 아니라 자기가 원하는 숫자를 찾으면 끝나니까 뭐부터 알아?85를 외우고 바로 찾기 전에 있으면 바로 찾는다 보통 정령이 되어 있으면 찾는데 낙85를 찾는다 = 절반을 나누는 중간에 있는 값이 말이죠. 정렬되어 있으면 아네가 그래서 이진 탐색 오름 순서로 데이터 정렬 중간 수사자와 K 비교한 후라면 탐색 성공 k가 작으면 이전 클래스에서 같은 방법으로 K를 찾고, K가 크면 후 클래스에서 같은 방법으로 K를 찾는다.물건을 사서 거스름돈으로 받아야 한다면? 가장 작은 수의 코인 수를 원합니다.GIF 싫어하시죠? 거의 없죠? 그래서 우리는 가장 적은 물 소고기 덮밥을 원해요.거스름돈이 10원이면 730원짜리 자리에 73개 넣는 건 어렵겠죠? 주머니에 그래서 제일 적은 수의 개수로 주는 거 500원이면 10원짜리 자리 하나에 200원, 730원, 3개 총 6개 받는 게 최소죠?알고리즘으로?이걸가지고해결하는알고리즘을보는데,동전=그리고GREDDY알고리즘이라고합니다.그래서 최대로 욕심을 내서 최대 액면의 코인을 계속 고르는 것, 그래서 최적화 알고리즘이라고도 합니다. 그러면 나중에 더 할 수 있어요.프로그래밍 언어를 배우면 이동 전에 거스름돈 프로그래밍을 짤 수 있습니다.가장 큰 액면의 코인으로 개수를 누설하기만 하면 돼요, 그래서 아이가 그리디 알고리즘이에요.네번째를보시면한필쓰기인데요.종이에서 연필을 떼지 않도록 – 리기 있는 그림을 가지고 한번에 그림의 어떤 한 점에서 출발해서 모든 선을 한 번만 지나서 출발하는 점으로… 연필이 종이에서 떨어지면 안 된다.몇 번 방문해도 상관없어.선은 중복되어서는 안됩니다.그래서 한 번 더 선은 한 번만 = 그런데 번호를 쓰는 대로 했는데 점은 중복이고 점을 지나는 것은 오일러 서킷 알고리즘 = 현재점으로 돌아가는 사이클이 있으면 진행한다.외길이면, 즉 인접한 점이 하나밖에 없으면 사이클 체크 없이 인저반점으로 간다.다섯 번째 미로 찾기입니다.미로찾기란 오른손의 법칙이라고 합니다.그리스 신화에 나오는데 지중해 그레타섬이 통치한 폭군 미노스왕인데 황소의 머리에 하체는 사람인 무서운 짐승 미노타울에게 제물을 바치기 위해 아테네에 젊은 남녀ㄴ의 제물로 요구=지하에 미로가 있는데 이 미로 속에 넣습니다.탈출하지 못하면 미노타우르에게 잡아먹히면 아테네의 한 젊은 청년 테세우스는 제물이 된다며 칼과 실을 들고 미로에 들어가 실을 풀고 미노타우로 몬스터를 들고 미로에 들어가 이 미로를 휘저으며 이 미로를 빠져나갔다.그리고 이 청년이 구미로가 얼마나 큰지 모르고, 그런데 실을 가져간다=그러면 구미로에서 찾을 수 있구나 하는 알고리즘을 생각해낸다.=약간 맞지 않는, 그래서 명탐정 코난인 어린 친구들끼리, 한 여학생의 유산 상속을 위해서 수수께끼의 물건 = 미로를 풀어 입던 옷에 실을 풀고 미로를 찾는 것은 같고, 이것도 하나의 문제 해결이 될 것 같다는 거죠, 아이는 어떤 것인가?오른손 법칙이에요, 대부분 실이 없어.그럼 어떻게 나와?오른손 법칙 미로에서 오른손을 대고 나옵니다.근데 그리스 신화에서는 어두워서 불가능해요.지하 미로라면 불가능, 그러면 출구가 나올 때까지 오른손으로 댐을 계속 오른쪽으로 가니까 출구까지 나올 수도 있어. 그런데 이것도 안 맞을 수도 있어. 벽이 그냥 벽이면 좋겠지만 그래도 최선의 방법이다.미로가 끊길 수 있습니다.>그럼 동전 찾기 = 가짜 동전은 눈으로 식별 불가능, 가짜 동전의 무게는 일반 동전보다 조금 가볍다, 그럼 동전을 찾아보자.무게가 일반 코인보다 조금 가볍다면?그런 경우는 어떻게 할까.코인이 많고 저울이 있는 n, n-1 사용 가장 좋은 방식은 처음 찾는 것 249번 250번 이렇게 해당되는 경우 찾는 것이 최악, 그러니까 코인을 반으로 나누는 것 하나가 무겁다.가볍다 그러면 차이가 나면 그쪽이 이상한 잔돈이니까 어떡해?=또 나누기 ㅋㅋ 계속 나누기 마지막에 2개가 남으면 가짜 동전을 가려낼 수 있으니 얼마나 좋은 아이디어야?! 인가 log102=10rem 그래도 만약 코인 n개가 있다면 log2n번 저울에 달면 가짜 동전을 찾을 수 있다.이 알고리즘 비교하면 어떨 때 커진다.100만개라고 하면 2의 log2n번 저울에 올리면 가짜 동전을 찾을 수 있습니다.이걸 수학적인 부분이라고 하죠? 알고리즘을 가지고 하나씩 보면, 두 알고리즘의 시간 복잡도는 log2의 n곱이다, 무슨 표기법 worst choice = 1023번 저울에 거는 better choice = 512번 포함 Best choice = 10번이면 가짜 동전을 찾는다. 다음은 n이 커질수록 커지고 n이 작으면 머리가 나빠질 수 있다.동전의 개수가 많을수록 커진다.//독이라도 술항아리 =혜탐색 부분의 입력을 줄였다가 늘려주는 것, 일단 술항아리 한 명이 하나만 마시고 일주일 뒤에 살면 그 사람은 독이 들어가지 않더라도 이것이 가장 희생수가 적어야 하는데 어떻게 해야 하는지…4개의 항아리를 두 그룹으로 나누어 한 사람이 두 개의 손을 쓴다, 이것은 이렇게 말하지 않으면 이를 이용해 문제를 푼다, 네 개의 항아리 중 하나를 두 신하에게 동시에 맛본다, 하나는 맛을 보지 않고 신하 하나, 둘이 넷째 술싱하 두 번째가.이걸 합쳐서 먹을 사람을 주문하는 경우의 수 같은데 찾을 수 있겠죠? 경우의 수로 나오는데 00110110111DA DBDCBDCBADlr이 이를 수행할 수 있는 희생자 수는 =0~log2N이라고 한다.그래서 N 명명 필요 // 저울을 한 번만 사용해서 가짜 약통이 든 것을 찾을 경우 10개 중 1개가 가짜 한 개 무게가; 수학이 사탕처럼 안 되는 문제 억지로 만드는 초등학생 때 달력이 뭔가 찢어지거나 (아니 상식적으로 책을 왜 그렇게 보관해?) = 그래서 뭘 어떻게 해? 응. 내가 생각해도 9개를 해도 안 되니까 약통을 다 열어볼까?아니면 운이 좋으면 되는데 아무리 생각해도 내 IQ로는 불가능할 것 같아.아니, 저울이 비교저울이라면 몰라도 돼지고기를 한 근 잴 때 쓰는 그런 저울이면 어떨까. 이걸 약을 다 먹더라도 아니, 더 무겁다고 했으니까 다 올려놔?그럼 아캬 아니야? 그럼 하나를 배?9개 선택? 잠깐만, 9개.